Topological Effects in 2D Materials
Atomically thin materials such as graphene, are ideal systems to study electronic states in two dimensions. Topological physics in 2D systems manifests itself as 1D conduction channels at the sample edges. Microwave Impedance Microscopy, as a spatially resolved technique, can provide direct insights on the electronic states both at the edges and inside the bulk. MIM measurement in 2D topological systems has a few unique aspects: 1) MIM can probe sub-surface features, suitable for studying high quality samples with protective capping layers. 2) MIM and transport can be performed simultaneously on the same Hall bar structure. This offers a meaningful comparison of the two measurements, which provides a comprehensive understanding of the underlying physics.
-
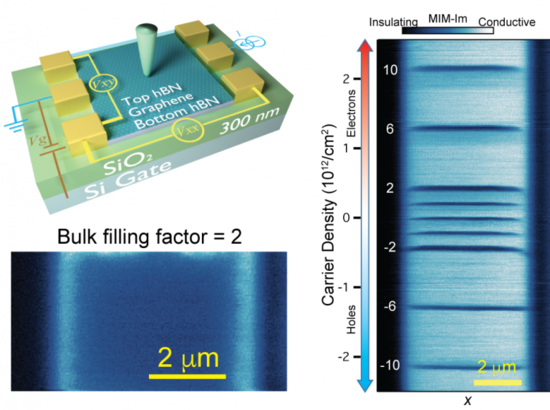
Quantum Hall Effects
QH effects are due to the formation Landau levels (LLs) in 2D systems under strong magnetic fields. The figure shows the MIM study of QH effects in monolayer graphene. The edge states are clearly observed as the bulk goes through a transition when LLs are completely filled. The carrier density in the graphene can be easily tuned by electrostatic gating so that we can use MIM to resolve the LL structure throughout the graphene region. More details can be found at PRL 117, 186601 (2016).
-
Quantum Spin Hall Effects
QSH effects are realized in 2D topological insulators. Recently, monolayer WTe2 has been demonstrated as the first atomically thin QSH insulator. MIM imaging on this material directly confirms the existence of the edge conduction and its behaviors are fully consistent with expectations for a 2D TI. MIM further reveals interesting features such as the interal conduction lines inside the sample bulk. More details can be found at Sci. Adv. eaat8799 (2019).
-
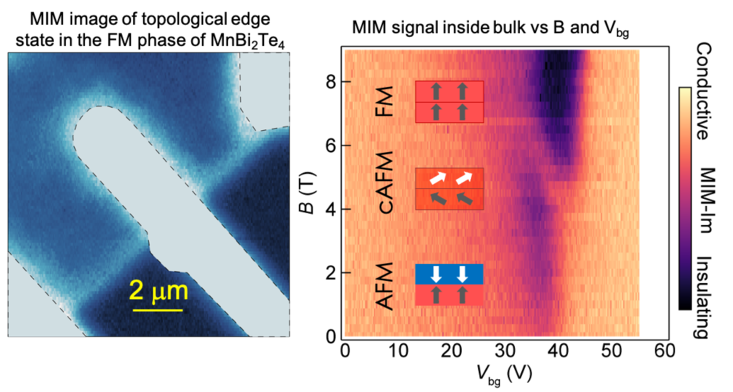
Magnetic Topological Insulators
Coupling topological physics with magnetism leads to a new class of topological materials known as Chern insulators. In a newly discovered magnetic topological insulator, MnBi2Te4, the topological properties are closely coupled to the magnetic states. Using MIM to map the bulk conductivity as a function of both magnetic field and gate voltage, we find that a conductive feature splits off from the conduction band, crosses the bulk gap, and eventually merges with the valence band, as the system is tuned from antiferromagnetic (AFM), to canted AFM, and to the FM state at high fields. Such band crossing feature is a key evidence for the topological phase transition in this system. More details can be found at Nano Lett. 21, 6, 2544–2550 (2021).